numpy.random.RandomState.noncentral_f

method

RandomState.noncentral_f(dfnum, dfden, nonc, size=None)

Draw samples from the noncentral F distribution.

Samples are drawn from an F distribution with specified parameters, dfnum (degrees of freedom in numerator) and dfden (degrees of freedom in denominator), where both parameters > 1. nonc is the non-centrality parameter.

Note

New code should use the noncentral_f method of a default_rng() instance instead; see random-quick-start.

Parameters

dfnumfloat or array_like of floats

Numerator degrees of freedom, must be > 0.

Changed in version 1.14.0: Earlier NumPy versions required dfnum > 1.

dfdenfloat or array_like of floats

Denominator degrees of freedom, must be > 0.

noncfloat or array_like of floats

Non-centrality parameter, the sum of the squares of the numerator means, must be >= 0.

sizeint or tuple of ints, optional

Output shape. If the given shape is, e.g., (m, n, k), then m * n * k samples are drawn. If size is None (default), a single value is returned if dfnum, dfden, and nonc are all scalars. Otherwise, np.broadcast(dfnum, dfden, nonc).size samples are drawn.

Returns

outndarray or scalar

Drawn samples from the parameterized noncentral Fisher distribution.

See also

Generator.noncentral_f

which should be used for new code.

Notes

When calculating the power of an experiment (power = probability of rejecting the null hypothesis when a specific alternative is true) the non-central F statistic becomes important. When the null hypothesis is true, the F statistic follows a central F distribution. When the null hypothesis is not true, then it follows a non-central F statistic.

References

1

Weisstein, Eric W. “Noncentral F-Distribution.” From MathWorld–A Wolfram Web Resource. http://mathworld.wolfram.com/NoncentralF-Distribution.html

2

Wikipedia, “Noncentral F-distribution”, https://en.wikipedia.org/wiki/Noncentral_F-distribution

Examples

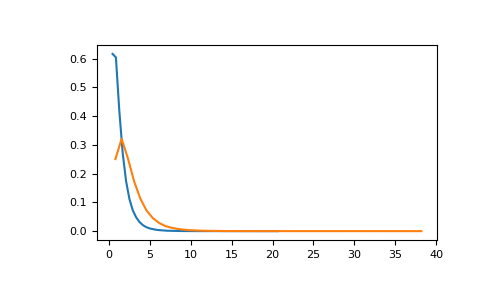
In a study, testing for a specific alternative to the null hypothesis requires use of the Noncentral F distribution. We need to calculate the area in the tail of the distribution that exceeds the value of the F distribution for the null hypothesis. We’ll plot the two probability distributions for comparison.

>>> dfnum = 3 # between group deg of freedom
>>> dfden = 20 # within groups degrees of freedom
>>> nonc = 3.0
>>> nc_vals = np.random.noncentral_f(dfnum, dfden, nonc, 1000000)
>>> NF = np.histogram(nc_vals, bins=50, density=True)
>>> c_vals = np.random.f(dfnum, dfden, 1000000)
>>> F = np.histogram(c_vals, bins=50, density=True)
>>> import matplotlib.pyplot as plt
>>> plt.plot(F[1][1:], F[0])
>>> plt.plot(NF[1][1:], NF[0])
>>> plt.show()